Математическая постановка задачи синтеза учебных планов вузов
Пусть все возможное содержание обучения представлено в виде множества дисциплин, которые, в свою очередь, состоят из учебных модулей.
; 
; 
(1.9)
где a(i,j) - j-й модуль i-й дисциплины;
N - количество дисциплин;
m(i) - количество модулей в i-й дисциплине.
Суммарный объем всех учебных модулей превышает допустимый объем учебного плана.
Учебным планом (УП) на d дискретных интервалах времени будем называть множество:
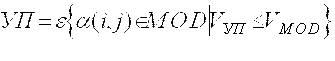(1.10)
где 
- объем всех модулей множества MOD;
- объем модулей, принадлежащих подмножеству учебного плана.
Тогда учебным планом будет являться некоторое подмножество множества MOD, суммарный объем модулей которого не превышает допустимый объем учебного плана.
Задача составления (синтеза) учебного плана сводится к следующему. Первоначально имеется объем дисциплин, превышающий объем учебного плана. Составить учебный план - это значит выбрать из всего объема дисциплин наиболее важные для данной специальности и расположить их по семестрам оптимальным, в смысле выбранного критерия, образом.
Для построения решения задачи синтеза введем дискретную единицу. Учебный год разбит на две части - осенний и весенний семестр. Весенний семестр содержит 17 недель, осенний - 18 (14) недель. При условии, что каждая дисциплина изучается в течение всего семестра, в качестве модуля минимального объема удобно выбирать раздел, соответствующий проведению одного часа занятий в неделю в течение семестра. Поэтому в качестве стандартного модуля можно выбрать модуль с объемом, кратным 17 часам. Небольшие отклонения от стандартного объема (в частности, при длине семестра 14 недель) несущественны [64].
Времена начала и окончания j-го семестра обозначим за n(j) и k(j). Они представляют собой номера недель с учетом каникул. Отсчет будем вести с нулевой недели, т.е. начало первого семестра n(1)=0.
Модули учебного плана взаимосвязаны, т.е. в последующих используется материал из ранее изученных модулей. Если модуль a(j,r) использует сведения из модуля a(i,l), то a(i,l) называется предком по отношению к a(j,r), а a(j,r) называется потомком по отношению к a(i,l) [17]. Каждой дуге, связывающей модули, ставится в соответствие некоторое число, отражающее тесноту связи. Тогда имеем некоторый граф, называемый графом содержательных связей (ГСС) [32].
Тесноту связи P(i,l;j,r) между модулями a(i,l) и a(j,r) можно охарактеризовать, оценив, какая часть всего лекционного материала из модуля a(i,l) используется в лекционном материале модуля a(j,r). Метод оценки этого коэффициента будет приведен далее в разделе 2.2.
Исходя из вышесказанного, модуль a(i,l) можно представить как набор параметров и функций:
a(i,l)={x(i,l,1), x(i,l,2), x(i,l,3), x(i,l,4), x(i,l,5), x(i,l,6), х(i,l,7), x(i,l,8), х(i,l,9), x(i,l,10), F(i,l,1), F(i,l,2)} (1.11)